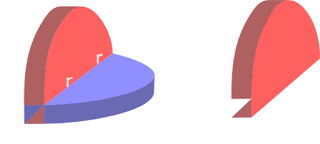ACM ICPC Regional Harbin 2010 - Volume

Entah mengapa saya merasa kasihan dengan soal ini, sehingga saya memutuskan untuk membahasnya. Soal yang akan dibahas dapat anda akses di Live Archive dengan kode 5096 (LA 5096).

Singkatnya, soal ini ingin kita untuk menghitung volume dari bangun berikut, dengan tinggi silinder dan jari-jarinya diberikan:

Gambar dari https://icpcarchive.ecs.baylor.edu

Untuk menyelesaikan soal ini, dibutuhkan pengetahuan tentang integral. Misalkan jari-jari silinder itu r dan tingginya h. Terdapat dua macam kasus, yaitu ketika 2r ≤ h, dan ketika 2r > h (bentuknya menjadi berubah).

Pertama, kita anggap 2r ≤ h sehingga bentuknya persis seperti yang ditunjukkan gambar di atas. Ambil $\frac{1}{8}$ bagian dari bangun itu, sehingga didapatkan bentuk berikut:

Kita cukup mencari volume dari bangun ini, lalu dikali dengan 8. Volume dari bangun ini sama dengan volume dari 2 kali $\frac{1}{4}$ silinder dikurangi dengan volume daerah di daerah perpotongannya. Daerah perpotongan itu memiliki bentuk seperti gambar warna ungu, dan memiliki tampak samping seperti bentuk berwarna merah:

Dengan menganggap bidang s bergeser dari atas ke bawah (yaitu dengan menjalankan x=0 sampai x=r), volume dari bangun perpotongan itu adalah:
$\begin{eqnarray*} \int_0^r \! s^2 \, \mathrm{d}x &=& \int_0^r \! \left(\sqrt{r^2 - x^2}\right)^2 \, \mathrm{d}x\\ &=& \int_0^r \! r^2 - x^2 \, \mathrm{d}x\\ \end{eqnarray*}$
Integral tersebut diselesaikan dengan substitusi trigonometri

Misalkan $x = r\sin{\theta}$, maka $\mathrm{d}x = r\cos{\theta}\ \mathrm{d}\theta$
Perhatikan bahwa batas-batas integral kita masih dalam $x$, bukan $\theta$. Untuk itu, kita perlu melakukan perubahan.

Untuk batas bawah:
$\begin{eqnarray*} 0 &=& r \sin{\theta}\\ 0 &=& \sin{\theta}\\ \theta &=& 0\\ \end{eqnarray*}$

Untuk batas atas:
$\begin{eqnarray*} r &=& r \sin{\theta}\\ 1 &=& \sin{\theta}\\ \theta &=& \pi/2\\ \end{eqnarray*}$

Substitusikan ke dalam persamaan:
$\begin{eqnarray*} \int_0^r \! r^2 - x^2 \, \mathrm{d}x &=& \int_0^{\pi/2} \! \left( r^2 - r^2\sin^2{\theta}\right) r \cos{\theta}\ \mathrm{d}\theta\\ &=& \int_0^{\pi/2} \! r^3 (1 - \sin^2{\theta}) \cos{\theta}\ \mathrm{d}\theta\\ &=& r^3 \left( \int_0^{\pi/2} \! \cos{\theta}\ \mathrm{d}\theta - \int_0^{\pi/2} \! \sin^2{\theta}\cos{\theta}\ \mathrm{d}\theta\right) \\ &=& r^3 \left( \left[\sin{\theta}\right]_0^{\pi/2} - \left[\frac{1}{3}\sin^3{\theta}\right]_0^{\pi/2} \right)\\ &=& r^3 \left( 1 - \frac{1}{3} \right)\\ &=& \frac{2}{3}r^3\\ \end{eqnarray*}$

Jadi kita sudah dapatkan volume dari bagian perpotongan kedua silinder tersebut. Volume keseluruhannya adalah 8 dikali, luas 2 kali 1/4 tabung dikurangi daerah yang tumpang tindih:
$\begin{eqnarray*} V &=& 8\left( 2\frac{1}{4}\pi r^2 h - \frac{2}{3}r^3 \right) \\ &=& 2\pi r^2 h - \frac{16}{3}r^3\\ \end{eqnarray*}$

Sekarang kita beranjak ke kasus berikutnya, ketika 2r > h. Anda dapat membayangkan bentuknya seperti dua koin yang menyatu di bagian tengah. Seperempat dari bangun tersebut berbentuk seperti gambar di kiri:

Volume dari bangun tersebut adalah dua kali volume bagian yang berwarna merah atau biru. Sementara volume bangun keseluruhan adalah empat kali dari bangun tersebut. Kita akan mencari volume bangun berwarna merah. Volumenya sama dengan volume setengah silinder itu dikurangi dengan volume daerah yang dipotong.

Volume yang dipotong adalah:
$\begin{eqnarray*} 2 \int_0^{h/2} \! x s \, \mathrm{d}x &=& 2 \int_0^{h/2} \! x \sqrt{r^2 - x^2} \, \mathrm{d}x\\ \end{eqnarray*}$
Seperti pada cara yang sebelumnya, kita gunakan substitusi trigonometri.
$\begin{eqnarray*} 2 \int_0^{h/2} \! r\sin{\theta} \sqrt{r^2 - r^2 \sin^2{\theta}} \, r\cos{\theta}\ \mathrm{d}\theta &=& 2 \int_0^{h/2} \! r^3 \sin{\theta}\cos^2{\theta} \, \mathrm{d}\theta\\ &=& 2\left[ -\frac{1}{3} r^3 \cos^3{\theta} \right]_0^{h/2} \\ &=& -\frac{2}{3}\left[ r^3 \cos^3{\theta} \right]_0^{h/2} \\ \end{eqnarray*}$

Ups, batas integral masih dalam $x$. Akan lebih mudah jika $\theta$ dikembalikan ke $x$. Perhatikan bahwa $r\cos{\theta} = \sqrt{r^2 - x^2}$. Jika disubstitusi:
$\begin{eqnarray*} -\frac{2}{3}\left[ r^3 \cos^3{\theta} \right]_0^{h/2} &=&-\frac{2}{3}\left[ (r^2 - x^2)^{3/2} \right]_0^{h/2}\\ \end{eqnarray*}$

Berhubung kalau dibuka ke bentuk tertutup rumusnya akan memusingkan, jadi saya biarkan dalam bentuk dengan batas atas dan bawah saja.

Volume akhir dari kasus kedua ini adalah 4 dikali 2 dikali, volume setengah silinder yang dikurangi bagian terpotong:
$\begin{eqnarray*} V &=& 4 \left( 2\left( \left( \frac{1}{2}\pi r^2 \frac{1}{2}h \right) - \left( -\frac{2}{3}\left[ (r^2 - x^2)^{3/2} \right]_0^{h/2} \right) \right) \right)\\ &=& 8\left( \frac{1}{4} \pi r^2 h +\frac{2}{3}\left[ (r^2 - x^2)^{3/2} \right]_0^{h/2}\right)\\ \end{eqnarray*}$

Yap, rumus sudah didapatkan. Selanjutnya tinggal diaplikasikan ke program.

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

#include <cstdio> #include <algorithm> #include <cmath> #include <cstring> #include <string>   using namespace std;   double A,B; double R,H;   double g(double x){   return pow(R*R-x*x,(double)1.5); }   int main(){    int r,h;    double K = (double)16/3;    double PI = acos((double)-1);    while (scanf("%d%d", &r, &h) == 2){     R=r;     H=h;       if (h >= 2*r){       printf("%.4lf\n", (2*PI*R*R*H - K*R*R*R));     }else{       A = (double)0.25*h*R*R*PI;       B = (double)2./3.*(g(0.5*h)-g(0));       printf("%.4lf\n", 8*(A+B));     }   }      return 0; }

Mau Dibawa ke Mana Bahasa Indonesia?

Tulisan kali ini tidak ada sangkut pautnya dengan competitive programming, hanya merupakan tuangan dari pikiran saya tentang kondisi berbahasa di negeri ini.

Prakata: tulisan ini hanyalah pikiran yang pernah melintas di kepala saya. Tidak ada maksud melawan, menjelek-jelekkan, atau sejenisya.

"... ciyuss? Miapah!?! Enelan?!??!"
"... gitu lho bro konsep kita, gimahow?"
"selaww brayy, kumpul masih minggu depan..."
"ini tuh gak make sense banget deh..."
"... gimana dong? Secara gue ini kan..."

Kata-kata yang kadang saya dengar entah di acara/iklan televisi, percakapan anak muda, baca di tweet seseorang, atau di status facebook. Terus terang, kata-kata itu membuat pikiran saya melayang-layang.

Beberapa waktu yang lalu, saya membaca sebuah artikel di entah situs apa (saya lupa). Artikel itu memberi komentar atas generasi muda yang yang sudah tidak lancar lagi berbahasa Indonesia. Artikel itu juga menyatakan di sekolah, mayoritas mereka menggunakan bahasa Inggris. Komentar itu juga dikaitkan dengan Sumpah Pemuda, bahwa para pemuda di masa lalu tidak main-main dalam menyatakan Bahasa Indonesia sebagai bahasa nasional.

Secara pribadi, saya setuju dengan maksud yang ingin disampaikan artikel itu. Jika anda bangsa Indonesia, hendaknya mampu berbahasa Indonesia dengan baik. Urusan bahasa sehari-hari tidak terlalu dipermasalahkan, entah itu bahasa Jawa, Sunda, Batak, atau bahasa daerah lainnya. Urusan sekolah mau belajar bahasa apa terserah, yang penting muridnya (yang bangsa Indonesia) mampu berbahasa Indonesia dengan baik.

Masalah muncul ketika yang dimaksudkan adalah berbahasa Indonesia, tetapi yang diucapkan adalah "bahasa" Indonesia. Entah dari mana sumbernya tetapi "bahasa" Indonesia hibrida mulai bermunculan. Sebut saja ciyus, enelan, dan kawan-kawannnya. Yang lebih lucu lagi adalah gimahow, selaw, bray. Bahasa apa itu!?

Sebelum saya mengenal kata-kata tersebut, saya tidak menganggap bahwa bahasa "gaul" merupakan sesuatu yang buruk. Sayangnya keberadaan kata-kata itu mulai mengancam kedudukan bahasa "gaul" di zona-aman-digunakan. Apakah kata-kata seperti itu bermakna? Apakah menggunakan kata-kata seperti itu akan membuat seseorang terlihat gaul? Apakah berkomunikasi dengan setengah bahasa Inggris setengah bahasa Indonesia membuat seseorang terlihat keren?

Sungguh lucu apabila di masa depan kata-kata tersebut masuk ke dalam KBBI, dianggap sebagai kata-kata serapan. Bagaimanapun juga, saya tidak tahu apakah ini merupakan salah satu bentuk evolusi bahasa, fenomena yang wajar, atau hanya tren sesaat. Menurut saya, sebisa mungkin gunakan bahasa Indonesia jika memang ada kata untuk mewakili apa yang ingin disampaikan. Dalam menulis blog, saya sendiri berusaha menghindari penggunaan kata-kata bahasa asing, kecuali jika kata tersebut memang lazim digunakan untuk merepresentasikan maksud saya. Mengapa menggunakan thanks jika kita punya terima kasih, atau setidaknya "makasih"?

UVa 12440 - Save the Trees

Soal menarik yang akan dibahas kali ini adalah UVa 12440 - Save the Trees. Sedikit sekali diskusi yang ada di internet tentang soal ini, sehingga saya memutuskan untuk menulis pembahasannya.

Persoalannya adalah, diberikan sebuah barisan pohon (bisa sampai 100000) dengan ketinggian dan jenis tertentu. Tugas kita adalah mengelompokkan pohon-pohon konsekutif ke dalam beberapa grup, dimana banyakya grup tidak dibatasi dan di dalam grup tidak boleh ada pohon berjenis sama. Biaya untuk mengelompokkan sebuah grup sama dengan tinggi maksimum dari pohon di grup tersebut. Berapa biaya total minimal yang mungkin untuk mengelompokkan semua pohon tersebut?

Misalnya tinggi pohon ke-i dinyatakan dengan h[i], dan jenis pohon ke-i adalah c[i].
Observasi 1:
Untuk setiap pohon ke-i, ada pohon x dimana x adalah minimal dan x ≤ i, sedemikian sehingga c[j] untuk x ≤ j ≤ i unik. Kita sebut x ini sebagai pre[i].

UVa 10271 - Chopsticks

Soal menarik kali ini bersumber dari UVa 10271 - Chopsticks. Karena tidak banyak orang yang membahas soal ini di internet, maka saya akan membahasnya. Sedikit curhat, pertama kali saya membaca soal ini adalah pada tahun 2010. Pada saat itu saya benar-benar tidak ada ide bagaimana mengerjakannya. Di tahun 2011 akhir akhirnya saya kembali menantang soal ini, dan akhirnya accepted :D

Tugas: diberikan N batangan sumpit dengan panjang tertentu. Bentuk K triplet sumpit sedemikian sehingga biayanya seminimal mungkin. Biaya membentuk sebuah triplet sumpit sama dengan kuadrat dari selisih dua sumpit terpendek.

Misalkan kita tidak perlu mencari sumpit terpanjang untuk setiap set. Persoalan kita sekarang adalah:
Diberikan N bilangan. Buat K pasangan bilangan sedemikian sehingga jumlah kuadrat dari selisih mereka seminimal mungkin! Untuk kemudahan, anggap saja kita ingin meminimalkan biaya pemilihannya.

tokilearning - Webs

Update 2017-06-14:
Web tokilearning yang lama sudah tidak aktif, Anda sudah tidak bisa mengumpulkan jawaban untuk soal ini. Namun Anda masih dapat mempelajarinya di tulisan ini.

Oke kali ini saya akan membahas soal Webs dari tokilearning. Konon katanya soal ini digunakan untuk simulasi Pelatnas 2 TOKI 2010 di UGM. Dari gaya bahasanya, kelihatannya soal ini dibuat oleh Irvan Jahja. Sekilas, soal ini tampak menyeramkan. Pada kenyataannya tidak terlalu menyeramkan, asal kita memilah-milah dan tahu apa yang harus dikerjakan.

Tugas kita adalah menghitung berapa banyak segitiga yang ada!