Sudah lama sekali sejak saya menulis soal untuk TOKI Open Contest, mungkin sekitar tiga tahun lamanya. Bulan Oktober yang lalu, saya ditawarkan untuk menulis soal untuk TOKI Open Contest Desember dengan tema geometri. Solusi untuk semua soal di bawah ini bisa Anda unduh dari sini. Langsung saja saya bahas soalnya satu per satu.
Catatan: tulisan ini mengandung istilah dalam computational geometry, seperti vektor, cross product, convex hull, dan sebagainya. Anda diharapkan sudah memahaminya terlebih dahulu. Oh ya, ini juga menginspirasi saya untuk menulis tentang dasar-dasar dalam computational geometry. Kemungkinan besar akan saya tulis di kemudian hari.
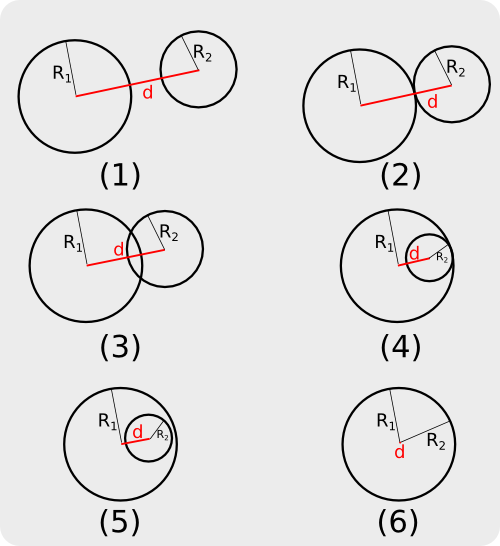
Misalkan d menyatakan jarak antar titik pusat lingkaran, R1 menyatakan jari-jari lingkaran yang lebih besar, dan R2 menyatakan jari-jari lingkaran yang lainnya. Kemungkinan-kemungkinannya adalah:
Salah satu solusi adalah dengan randomized algorithm. Idenya adalah kita bangkitkan N vektor secara acak yang jumlahnya vektor 0, dan tidak ada dua vektor yang memiliki vektor satuan yang sama. Kemudian urutkan menurut sudutnya ke sumbu-x positif. Jika vektor yang kita miliki adalah (x1, y1), (x2,y2), ..., (xN, yN), maka titik-titik yang menjadi lokasi tiang pancang adalah (x1, y1), (x1+x2, y1+y2), (x1+x2+x3, y1+y2+y3), ....
Bagaimana cara membangkitkan N vektor yang jumlahnya 0? Anggap N genap, bangkitkan N/2 vektor secara acak yang komponennya (x dan y) hanya terdiri dari bilangan positif, lalu N/2 vektor sisanya adalah negasi dari N/2 vektor yang awalnya sudah kita bangkitkan. Jika N ganjil, tambahkan vektor (0,1) dan kurangi komponen y dari vektor manapun.
Bagaimana cara memastikan N vektor yang kita miliki tidak ada yang memiliki vektor satuan yang sama? Misalkan kita membuat sebuah vektor v = (x, y) secara acak. Bagi x dan y dengan fpb(x, y), misalnya menjadi x' dan y'. lalu tandai bahwa (x', y') sudah pernah ditemukan dan untuk ke depannya jangan lagi membuat vektor dengan (x', y'). Saya menggunakan STL set<pair<int,int> > pada C++ untuk membantu pencatatan vektor-vektor yang sudah dibuat. Solusi ini dapat Anda lihat pada berkas "kandang_baru2.cpp". Eksekusi untuk N = 100.000 adalah sekitar 0.7 detik di komputer saya.
*C(x,y): x kombinasi y
Mari mulai dengan brute force terlebih dahulu. Untuk setiap pasang titik, misalnya titik A dan B, hitung banyaknya titik yang segaris dengan A dan B. Misalnya terdapat x titik, artinya banyaknya triplet yang kolinier bertambah sebanyak x. Pada akhirnya, jawaban akhir perlu dibagi 3 karena setiap triplet terhitung sebanyak 3 kali. Untuk memeriksa apakah tiga titik segaris atau tidak bisa dilakukan dengan cross product.
Cara itu bekerja dalam O(N3), dan akan mendapatkan TLE. Untuk mempercepat, kita coba ubah strategi brute force: ketimbang untuk setiap pasang titik, bagaimana jika kita mencoba untuk setiap titik saja? Ternyata hal ini memunculkan ide baru.
Misalkan semua titik lainnya berada di atas titik yang kita pilih (pada gambar, bulatan berwarna merah). Urutkan semua titik lainnya menurut sudut pada koordinat polar, lalu "sapu" dari sudut 0 derajat ke 180 derajat. Kita bisa menghitung berapa banyak titik yang segaris pada suatu sudut. Jika terdapat x titik yang segaris pada suatu sudut, maka jawabannya bertambah sebanyak C(x,2). Pengurutan dalam dilakukan dalam O(N log N) dan penyapuan dalam O(N). Jika Hal ini dicoba untuk setiap titik, kompleksitas akhirnya adalah O(N2 log N), cukup untuk AC.
Dalam soal ini, sudah jelas bahwa hampir pasti ada titik lain di bawah titik yang kita pilih. Lalu bagaimana mengakalinya? Kenyataannya adalah kita bisa mengabaikan semua titik yang ada di bawah titik yang kita pilih, dan jawabannya justru menjadi benar. Karena triplet kolinier yang melibatkan titik-titik di bawah titik yang kita pilih pasti sudah dicari saat kita memproses (urutkan + sapu) titik-titik yang berada di bawah itu.
Saat menyapu dari kiri ke kanan, setiap kali menemui suatu titik, sebut saja titik P, kita akan menghitung banyaknya simbol "lebih dari" yang bisa dibentuk jika titik P menjadi "sudut" dari simbol "lebih dari".
Perhatikan gambar berikut:
Titik P dinyatakan sebagai bulatan merah. Jelas bahwa banyaknya simbol "lebih dari" yang bisa dibentuk adalah perkalian dari banyaknya titik yang ada di zona biru dengan zona hijau. Tentu saja, kita mengabaikan titik yang memiliki ordinat y sama dengan titik P, dan semua titik yang memiliki ordinat x lebih dari atau sama dengan P.
Masalah selanjutnya adalah bagaimana cara menghitung banyaknya titik di zona biru dan hijau. Kita membutuhkan suatu struktur data yang secara dinamis bisa melakukan:
Observasi:
Selalu ada solusi optimal yang mana seluruh pagarnya membentuk poligon konveks.
Bukti: jika solusi optimalnya menggunakan poligon tidak konveks, maka kita selalu bisa mengkonversi semua pagar itu menjadi poligon konveks. Perhatikan gambar berikut:
Berdasarkan observasi tersebut, convex hull dari titik-titik yang diberikan pastilah merupakan pagar terluar dari salah satu solusi optimal. Setelah dibuat convex hull, buang semua titik-titik yang menyusunnya, dan kita akan mendapatkan masalah yang serupa (dengan cakupan yang lebih kecil). Dengan begitu, kita bisa mengulangi proses ini terus menerus hingga kita tidak bisa membentuk pagar yang sepenuhnya menutupi vila.
Bagaimana cara memeriksa apakah pagar yang dibentuk menutupi vila? Masalah yang kita jumpai ini sebenarnya adalah: bagaimana memeriksa apakah suatu poligon sembarang ada di dalam suatu poligon konveks? Kembali, solusinya bisa dicapai dengan convex hull.
Anggap titik-titik penyusun dari kedua poligon itu sebagai himpunan titik-titik, kemudian cari convex hull dari titik-titik tersebut. Jika seluruh titik penyusun convex hull itu merupakan titik-titik pada poligon konveks (yang seharusnya diluar), artinya poligon sembarang itu sepenuhnya berada di dalam poligon konveks. Perhatikan gambar di bawah untuk visualisasinya.
Convex hull yang sekaligus memeriksa apakah vila sepenuhnya ditutupi pagar bekerja dalam O(M log (N+M)), dan maksimal terdapat M/3 pagar. Dengan demikian solusinya bekerja dalam O(M2 log (N+M)).
Catatan: tulisan ini mengandung istilah dalam computational geometry, seperti vektor, cross product, convex hull, dan sebagainya. Anda diharapkan sudah memahaminya terlebih dahulu. Oh ya, ini juga menginspirasi saya untuk menulis tentang dasar-dasar dalam computational geometry. Kemungkinan besar akan saya tulis di kemudian hari.
Dua Gelang
Perhatikan setiap kemungkinan kasus yang ada, dan hubungkan dengan jarak antar titik pusat dan jari-jari lingkarannya.Misalkan d menyatakan jarak antar titik pusat lingkaran, R1 menyatakan jari-jari lingkaran yang lebih besar, dan R2 menyatakan jari-jari lingkaran yang lainnya. Kemungkinan-kemungkinannya adalah:
- Kedua lingkaran saling lepas. Hubungannya adalah R1+R2 < d.
- Kedua lingkaran bertemu di satu titik, dan kedua lingkaran tidak saling mengandung (yang satu berada di dalam yang lainnya). Hubungannya adalah R1+R2 = d.
- Kedua lingkaran bertemu di dua titik. Hubungannya adalah R1+R2 > d.
- Kedua lingkaran bertemu di satu titik, dan lingkaran yang besar mengandung lingkaran yang kecil. Hubungannya adalah R1 = d+R2.
- Kedua lingkaran saling lepas, dan lingkaran yang besar mengandung lingkaran yang kecil. Hubungannya adalah R1 > d+R2.
- Kedua lingkaran bertemu di tak hingga banyaknya titik, artinya kedua lingkaran identik dan memiliki titik pusat yang sama. Hubungannya adalah R1 = R2 dan d = 0. Kasus ini sebenarnya bisa ditangani juga oleh hubungan pada kasus (4).
Kandang Baru
Untuk mengerjakan soal ini Anda dapat menggunakan kreativitas masing-masing. Solusi dari saya yang sederhana adalah membuat parabola. Ya, cukup:for i <- 1..N cetak(i, i*i)Tambahan pembahasan: "Bagaimana jika N bisa sampai 100.000?"
Salah satu solusi adalah dengan randomized algorithm. Idenya adalah kita bangkitkan N vektor secara acak yang jumlahnya vektor 0, dan tidak ada dua vektor yang memiliki vektor satuan yang sama. Kemudian urutkan menurut sudutnya ke sumbu-x positif. Jika vektor yang kita miliki adalah (x1, y1), (x2,y2), ..., (xN, yN), maka titik-titik yang menjadi lokasi tiang pancang adalah (x1, y1), (x1+x2, y1+y2), (x1+x2+x3, y1+y2+y3), ....
Bagaimana cara membangkitkan N vektor yang jumlahnya 0? Anggap N genap, bangkitkan N/2 vektor secara acak yang komponennya (x dan y) hanya terdiri dari bilangan positif, lalu N/2 vektor sisanya adalah negasi dari N/2 vektor yang awalnya sudah kita bangkitkan. Jika N ganjil, tambahkan vektor (0,1) dan kurangi komponen y dari vektor manapun.
Bagaimana cara memastikan N vektor yang kita miliki tidak ada yang memiliki vektor satuan yang sama? Misalkan kita membuat sebuah vektor v = (x, y) secara acak. Bagi x dan y dengan fpb(x, y), misalnya menjadi x' dan y'. lalu tandai bahwa (x', y') sudah pernah ditemukan dan untuk ke depannya jangan lagi membuat vektor dengan (x', y'). Saya menggunakan STL set<pair<int,int> > pada C++ untuk membantu pencatatan vektor-vektor yang sudah dibuat. Solusi ini dapat Anda lihat pada berkas "kandang_baru2.cpp". Eksekusi untuk N = 100.000 adalah sekitar 0.7 detik di komputer saya.
Segitiga Bebek II
Kita akan menggunakan strategi komplemen, yaitu semua kemungkinan dikurangi kemungkinan-kemungkinan yang tidak sah. Artinya, jawabannya adalah C(N,3) dikurangi triplet titik yang koliner (segaris). Bagaimana mencari banyaknya tiga titik yang kolinier secara cepat?*C(x,y): x kombinasi y
Mari mulai dengan brute force terlebih dahulu. Untuk setiap pasang titik, misalnya titik A dan B, hitung banyaknya titik yang segaris dengan A dan B. Misalnya terdapat x titik, artinya banyaknya triplet yang kolinier bertambah sebanyak x. Pada akhirnya, jawaban akhir perlu dibagi 3 karena setiap triplet terhitung sebanyak 3 kali. Untuk memeriksa apakah tiga titik segaris atau tidak bisa dilakukan dengan cross product.
Cara itu bekerja dalam O(N3), dan akan mendapatkan TLE. Untuk mempercepat, kita coba ubah strategi brute force: ketimbang untuk setiap pasang titik, bagaimana jika kita mencoba untuk setiap titik saja? Ternyata hal ini memunculkan ide baru.
Dalam soal ini, sudah jelas bahwa hampir pasti ada titik lain di bawah titik yang kita pilih. Lalu bagaimana mengakalinya? Kenyataannya adalah kita bisa mengabaikan semua titik yang ada di bawah titik yang kita pilih, dan jawabannya justru menjadi benar. Karena triplet kolinier yang melibatkan titik-titik di bawah titik yang kita pilih pasti sudah dicari saat kita memproses (urutkan + sapu) titik-titik yang berada di bawah itu.
Lebih Dari
Ada beberapa solusi yang bisa digunakan untuk soal ini. Solusi saya saya pakai adalah dengan menyapu dari kiri ke kanan. Sebenarnya istilah menyapu ini dikenal sebagai paradigma line sweep pada computational geometry, dan akan sering Anda jumpai jika Anda menggeluti computational geometry.Saat menyapu dari kiri ke kanan, setiap kali menemui suatu titik, sebut saja titik P, kita akan menghitung banyaknya simbol "lebih dari" yang bisa dibentuk jika titik P menjadi "sudut" dari simbol "lebih dari".
Perhatikan gambar berikut:
Masalah selanjutnya adalah bagaimana cara menghitung banyaknya titik di zona biru dan hijau. Kita membutuhkan suatu struktur data yang secara dinamis bisa melakukan:
- update(x), artinya menambah nilai di posisi x sebanyak 1.
- query(a,b), artinya menghitung jumlah nilai-nilai dari posisi a sampai dengan posisi b.
Pulau Komodo
Kita akan mengerjakannya dari belakang. Artinya, mulai dengan membangun pagar terluar sampai pagar terdalam. Dengan asumsi pagar yang kita bangun optimal, solusi ini akan sama optimalnya jika kita membangun pagar dari dalam dengan optimal.Observasi:
Selalu ada solusi optimal yang mana seluruh pagarnya membentuk poligon konveks.
Bukti: jika solusi optimalnya menggunakan poligon tidak konveks, maka kita selalu bisa mengkonversi semua pagar itu menjadi poligon konveks. Perhatikan gambar berikut:
Bagaimana cara memeriksa apakah pagar yang dibentuk menutupi vila? Masalah yang kita jumpai ini sebenarnya adalah: bagaimana memeriksa apakah suatu poligon sembarang ada di dalam suatu poligon konveks? Kembali, solusinya bisa dicapai dengan convex hull.
Anggap titik-titik penyusun dari kedua poligon itu sebagai himpunan titik-titik, kemudian cari convex hull dari titik-titik tersebut. Jika seluruh titik penyusun convex hull itu merupakan titik-titik pada poligon konveks (yang seharusnya diluar), artinya poligon sembarang itu sepenuhnya berada di dalam poligon konveks. Perhatikan gambar di bawah untuk visualisasinya.
Tidak ada komentar :
Posting Komentar