Dikenal juga sebagai struktur data Fenwick Tree
Saya sering menyebutkan struktur data ini pada tulisan-tulisan saya yang sebelumnya. Biasanya saya mencantumkan link ke halaman tutorial Fun Programming Club Ristek Fasilkom UI (organisasi semacam "klub programming"). Namun kini webnya sudah berubah, dan tulisan yang lama sudah menghilang. Untuk itu saya akan menuliskannya di blog ini.Struktur data ini memiliki kegunaan yang mirip dengan segment tree. Hal yang dapat dikerjakan BIT, dapat dikerjakan segment tree, tetapi belum tentu sebaliknya. Mari kita mulai dengan persoalan motivasi.
Persoalan Motivasi
Diberikan sebuah array A yang berisi N bilangan. Array A terdefinisi untuk A[1..N] (one-based). Terdapat sejumlah perintah yang masing-masing dapat berbentuk:- update(x, v), artinya tambah nilai di indeks x sebanyak v.
- query(x), artinya cari nilai A[1] + A[2] + ... + A[x].
Segment tree dapat dengan mudah menyelesaikan masalah ini, dengan update O(log N) dan query O(log N). Namun mari kita coba bahas dengan BIT.
Penyimpanan Data pada BIT
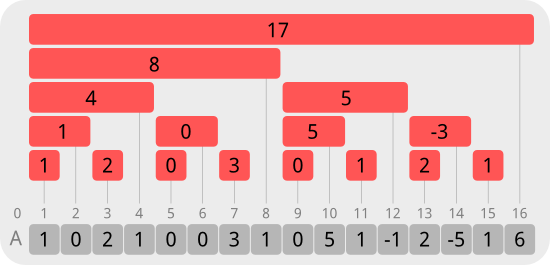
Seperti pada segment tree, BIT menggunakan konsep membagi pertanggungjawaban pada segmen-segmen yang lebih kecil. Pada BIT, bentuk tree-nya adalah sebagai berikut:Kotak-kotak abu-abu adalah array yang direpresentasikan, sementara batangan merah adalah segmen yang bertanggungjawab atas suatu interval.
Bentuknya tidak seperti tree. Bahkan saya tidak menggambar edge, karena saya juga tidak tahu di mana tree-nya. Namun yang penting untuk diperhatikan adalah segmen-segmennya.
Terdapat N segmen untuk membuat BIT dari array dengan ukuran N. Array ini harus dimulai dari indeks 1 (one-based). Perhatikan bahwa segmen bernomor x bertanggung jawab dalam menyimpan nilai agregat dalam array dengan indeks yang merupakan anggota [x−2d+1,x] dengan d adalah posisi bit 1 dari kanan yang ada di x.
Misalkan untuk 12, binernya adalah 1100, sehingga d = 2. Pada gambar, terlihat bahwa cakupan dari segmen nomor 12 adalah [12−22+1,12] = [9,12]. Sementara untuk 8, cakupannya adalah [8-23+1,8] = [1,8].
Untuk soal ini, nilai agregat adalah sesederhana jumlahan nilai yang dicakup segmen. Misalnya diketahui array A kini berisi beberapa nilai, berikut struktur BIT-nya:
Kotak-kotak abu-abu menyatakan array A. Nilai dalam segmen menyatakan nilai agregat yang dia simpan (mewakili elemen-elemen A pada intervalnya).
Untuk implementasinya, kita menyimpan nilai agregat dari segmen BIT pada sebuah array baru bernama bit. Jadi nilai dari segmen ke-i disimpan pada bit[i].
Operasi pada BIT
Perhatikan contoh operasi query dan gambar berikut:- Saat ditanya nilai dari A[1] + A[2] + ... + A[11], kita cukup jumlahkan bit[11], bit[10], dan bit[8].
- Bila yang ditanya nilai dari A[1] + A[2] + ... + A[15], kita cukup jumlahkan bit[15], bit[14], bit[12], dan bit[8].
Strategi ini dapat dituliskan sebagai fungsi rekursif. Untuk mencari query(x), yaitu A[1] + A[2] + ... + A[x], sama saja dengan mencari bit[x] + query(x−2d), dengan d seperti pada definisi sebelumnya. Mencari query(x−2d) sendiri nantinya akan dilakukan secara rekursif. Basis dari rekursi ini adalah ketika x=0, yang artinya sudah pasti tidak ada segmen yang perlu dijumlahkan.
Saat melakukan update, kita hanya perlu memperbaharui nilai-nilai pada segmen tertentu. Misalkan dilakukan update A[7] supaya nilainya ditambah dengan v, maka segmen 7, 8, dan 16 juga harus ditambah dengan v. Dengan kata lain, bit[7], bit[8], dan bit[16] perlu ditambahkan dengan v. Pada intinya, jika kita ingin melakukan update pada elemen ke-x, maka seluruh segmen yang terletak di atas segmen x perlu di-update juga.
Segmen terdekat yang mencakup segmen ke-x adalah segmen ke-(x+2d), dengan d seperti pada definisi sebelumnya. Setelah itu lakukan pula update secara rekursif pada segmen ke-(x+2d). Berhenti ketika segmen yang hendak di-update sudah tidak ada (melebihi N).
Dapat dibuktikan bahwa untuk setiap query atau update, paling banyak hanya ada O(log N) segmen yang diproses. Sehingga kompleksitas dari query dan update adalah O(log N). Sama dengan segment tree!
Implementasi
Meskipun teorinya agak rumit, BIT sangat mudah untuk diimplementasikan:
Secara mengejutkan, potongan kode di atas sudah melakukan segala pekerjaan dari BIT. Meskipun konsep yang saya jelaskan menggunakan rekursif, implementasinya juga dapat dilakukan secara iteratif seperti yang ditunjukkan kode di atas.
Kode yang pendek merupakan kelebihan dari BIT. Bandingkan dengan panjangnya kode segment tree! Rahasia utama pendeknya kode ada pada operasi (i & -i), yang fungsinya adalah mengekstrak bit 1 terakhir dari i. Detil mengapa potongan kode itu bisa berfungsi dengan baik tidak dijelaskan di bagian ini. Mungkin akan saya jelaskan di tulisan mendatang tentang operasi bit.
Cukup jelas bahwa banyaknya iterasi maksimal yang dilakukan fungsi update dan query adalah maksimal sebanyak panjang digit N dalam biner. Oleh karena itu kompleksitas untuk kedua operasi tersebut adalah O(log N). Memori yang digunakan juga cukup O(N).
Sebagai bonus, seluruh operasi pada BIT berlangsung secara iteratif. Selain itu hanya terdapat operasi penjumlahan, pengurangan, dan bitwise. Artinya, BIT memiliki konstanta yang sangat-sangat-sangat ringan jika dibandingkan dengan segment tree. Menurut pengalaman saya, BIT bisa jadi 10x lebih cepat dari segment tree.
Keterbatasan BIT
Anda telah melihat kesaktian BIT. Namun sebenarnya BIT cukup terbatas bila dibandingkan dengan segment tree. Semua operasi agregasi harus dilakukan dari interval 1 sampai dengan x, tidak seperti segment tree yang bisa sembarang interval. Kalau sekedar masalah range sum query untuk interval [a,b], BIT masih dapat menanganinya dengan mencari sum(1,b) dikurangi sum(1,a-1). Namun bagaimana untuk range minimum query suatu interval [a,b]? BIT tidak dapat menanganinya dengan sederhana, sebab nilai min(1,a-1) tidak dapat dibuang seperti pada kasus range sum query.Lazy propagation pada BIT juga tidak sederhana, walaupun memungkinkan.
Latihan
Sebagai latihan, Anda dapat mengerjakan:- SPOJ INVCNT. Petunjuk: proses dari belakang ke depan. Sebelumnya kompres elemennya terlebih dahulu, [1, 3, 4, 9] => [1, 2, 3, 4].
- SPOJ RATING (lebih sulit)
Penutup
Dibalik kekurangan bila dibandingkan dengan segment tree, BIT tetap merupakan struktur data yang sangat kuat. Kode yang pendek dan konstanta ringan membuat BIT memiliki niche* pada kompetisi pemrograman. BIT juga dapat dikomposisikan dengan struktur data lainnya.Tulisan ini juga merupakan pengantar dari tulisan saya yang akan datang, yaitu teknik khusus pada BIT. Ada juga kemungkinan tulisan ini dimuat pada training gate TOKI ke depannya.
*Catatan: dalam pelajaran biologi, niche adalah peran suatu organisme pada ekosistem. Misalnya niche bintang laut pada ekosistem perairan laut dalam adalah pengurai mayat dan zat organik di dasar laut.





Tidak ada komentar :
Posting Komentar