Entah mengapa saya merasa kasihan dengan soal ini, sehingga saya memutuskan untuk membahasnya. Soal yang akan dibahas dapat anda akses di Live Archive dengan kode 5096 (LA 5096).
Singkatnya, soal ini ingin kita untuk menghitung volume dari bangun berikut, dengan tinggi silinder dan jari-jarinya diberikan:
Untuk menyelesaikan soal ini, dibutuhkan pengetahuan tentang integral. Misalkan jari-jari silinder itu r dan tingginya h. Terdapat dua macam kasus, yaitu ketika 2r ≤ h, dan ketika 2r > h (bentuknya menjadi berubah).
Pertama, kita anggap 2r ≤ h sehingga bentuknya persis seperti yang ditunjukkan gambar di atas. Ambil \(\frac{1}{8}\) bagian dari bangun itu, sehingga didapatkan bentuk berikut:
Kita cukup mencari volume dari bangun ini, lalu dikali dengan 8. Volume dari bangun ini sama dengan volume dari 2 kali \(\frac{1}{4}\) silinder dikurangi dengan volume daerah di daerah perpotongannya. Daerah perpotongan itu memiliki bentuk seperti gambar warna ungu, dan memiliki tampak samping seperti bentuk berwarna merah:
Dengan menganggap bidang s bergeser dari atas ke bawah (yaitu dengan menjalankan x=0 sampai x=r), volume dari bangun perpotongan itu adalah:
\(
\begin{eqnarray*}
\int_0^r \! s^2 \, \mathrm{d}x &=& \int_0^r \! \left(\sqrt{r^2 - x^2}\right)^2 \, \mathrm{d}x\\
&=& \int_0^r \! r^2 - x^2 \, \mathrm{d}x\\
\end{eqnarray*}
\)
Integral tersebut diselesaikan dengan substitusi trigonometri
Misalkan \(x = r\sin{\theta}\), maka \(\mathrm{d}x = r\cos{\theta}\ \mathrm{d}\theta\)
Perhatikan bahwa batas-batas integral kita masih dalam \(x\), bukan \(\theta\). Untuk itu, kita perlu melakukan perubahan.
Untuk batas bawah:
\(
\begin{eqnarray*}
0 &=& r \sin{\theta}\\
0 &=& \sin{\theta}\\
\theta &=& 0\\
\end{eqnarray*}
\)
Untuk batas atas:
\(
\begin{eqnarray*}
r &=& r \sin{\theta}\\
1 &=& \sin{\theta}\\
\theta &=& \pi/2\\
\end{eqnarray*}
\)
Substitusikan ke dalam persamaan:
\(
\begin{eqnarray*}
\int_0^r \! r^2 - x^2 \, \mathrm{d}x &=& \int_0^{\pi/2} \! \left( r^2 - r^2\sin^2{\theta}\right) r \cos{\theta}\ \mathrm{d}\theta\\
&=& \int_0^{\pi/2} \! r^3 (1 - \sin^2{\theta}) \cos{\theta}\ \mathrm{d}\theta\\
&=& r^3 \left( \int_0^{\pi/2} \! \cos{\theta}\ \mathrm{d}\theta - \int_0^{\pi/2} \! \sin^2{\theta}\cos{\theta}\ \mathrm{d}\theta\right) \\
&=& r^3 \left( \left[\sin{\theta}\right]_0^{\pi/2} - \left[\frac{1}{3}\sin^3{\theta}\right]_0^{\pi/2} \right)\\
&=& r^3 \left( 1 - \frac{1}{3} \right)\\
&=& \frac{2}{3}r^3\\
\end{eqnarray*}
\)
Jadi kita sudah dapatkan volume dari bagian perpotongan kedua silinder tersebut. Volume keseluruhannya adalah 8 dikali, luas 2 kali 1/4 tabung dikurangi daerah yang tumpang tindih:
\(
\begin{eqnarray*}
V &=& 8\left( 2\frac{1}{4}\pi r^2 h - \frac{2}{3}r^3 \right) \\
&=& 2\pi r^2 h - \frac{16}{3}r^3\\
\end{eqnarray*}
\)
Sekarang kita beranjak ke kasus berikutnya, ketika 2r > h. Anda dapat membayangkan bentuknya seperti dua koin yang menyatu di bagian tengah. Seperempat dari bangun tersebut berbentuk seperti gambar di kiri:
Volume dari bangun tersebut adalah dua kali volume bagian yang berwarna merah atau biru. Sementara volume bangun keseluruhan adalah empat kali dari bangun tersebut. Kita akan mencari volume bangun berwarna merah. Volumenya sama dengan volume setengah silinder itu dikurangi dengan volume daerah yang dipotong.Singkatnya, soal ini ingin kita untuk menghitung volume dari bangun berikut, dengan tinggi silinder dan jari-jarinya diberikan:
Gambar dari https://icpcarchive.ecs.baylor.edu
Untuk menyelesaikan soal ini, dibutuhkan pengetahuan tentang integral. Misalkan jari-jari silinder itu r dan tingginya h. Terdapat dua macam kasus, yaitu ketika 2r ≤ h, dan ketika 2r > h (bentuknya menjadi berubah).
Pertama, kita anggap 2r ≤ h sehingga bentuknya persis seperti yang ditunjukkan gambar di atas. Ambil \(\frac{1}{8}\) bagian dari bangun itu, sehingga didapatkan bentuk berikut:
Kita cukup mencari volume dari bangun ini, lalu dikali dengan 8. Volume dari bangun ini sama dengan volume dari 2 kali \(\frac{1}{4}\) silinder dikurangi dengan volume daerah di daerah perpotongannya. Daerah perpotongan itu memiliki bentuk seperti gambar warna ungu, dan memiliki tampak samping seperti bentuk berwarna merah:
Dengan menganggap bidang s bergeser dari atas ke bawah (yaitu dengan menjalankan x=0 sampai x=r), volume dari bangun perpotongan itu adalah:
\(
\begin{eqnarray*}
\int_0^r \! s^2 \, \mathrm{d}x &=& \int_0^r \! \left(\sqrt{r^2 - x^2}\right)^2 \, \mathrm{d}x\\
&=& \int_0^r \! r^2 - x^2 \, \mathrm{d}x\\
\end{eqnarray*}
\)
Integral tersebut diselesaikan dengan substitusi trigonometri
Misalkan \(x = r\sin{\theta}\), maka \(\mathrm{d}x = r\cos{\theta}\ \mathrm{d}\theta\)
Perhatikan bahwa batas-batas integral kita masih dalam \(x\), bukan \(\theta\). Untuk itu, kita perlu melakukan perubahan.
Untuk batas bawah:
\(
\begin{eqnarray*}
0 &=& r \sin{\theta}\\
0 &=& \sin{\theta}\\
\theta &=& 0\\
\end{eqnarray*}
\)
Untuk batas atas:
\(
\begin{eqnarray*}
r &=& r \sin{\theta}\\
1 &=& \sin{\theta}\\
\theta &=& \pi/2\\
\end{eqnarray*}
\)
Substitusikan ke dalam persamaan:
\(
\begin{eqnarray*}
\int_0^r \! r^2 - x^2 \, \mathrm{d}x &=& \int_0^{\pi/2} \! \left( r^2 - r^2\sin^2{\theta}\right) r \cos{\theta}\ \mathrm{d}\theta\\
&=& \int_0^{\pi/2} \! r^3 (1 - \sin^2{\theta}) \cos{\theta}\ \mathrm{d}\theta\\
&=& r^3 \left( \int_0^{\pi/2} \! \cos{\theta}\ \mathrm{d}\theta - \int_0^{\pi/2} \! \sin^2{\theta}\cos{\theta}\ \mathrm{d}\theta\right) \\
&=& r^3 \left( \left[\sin{\theta}\right]_0^{\pi/2} - \left[\frac{1}{3}\sin^3{\theta}\right]_0^{\pi/2} \right)\\
&=& r^3 \left( 1 - \frac{1}{3} \right)\\
&=& \frac{2}{3}r^3\\
\end{eqnarray*}
\)
Jadi kita sudah dapatkan volume dari bagian perpotongan kedua silinder tersebut. Volume keseluruhannya adalah 8 dikali, luas 2 kali 1/4 tabung dikurangi daerah yang tumpang tindih:
\(
\begin{eqnarray*}
V &=& 8\left( 2\frac{1}{4}\pi r^2 h - \frac{2}{3}r^3 \right) \\
&=& 2\pi r^2 h - \frac{16}{3}r^3\\
\end{eqnarray*}
\)
Sekarang kita beranjak ke kasus berikutnya, ketika 2r > h. Anda dapat membayangkan bentuknya seperti dua koin yang menyatu di bagian tengah. Seperempat dari bangun tersebut berbentuk seperti gambar di kiri:
Volume yang dipotong adalah:
\(
\begin{eqnarray*}
2 \int_0^{h/2} \! x s \, \mathrm{d}x &=& 2 \int_0^{h/2} \! x \sqrt{r^2 - x^2} \, \mathrm{d}x\\
\end{eqnarray*}
\)
Seperti pada cara yang sebelumnya, kita gunakan substitusi trigonometri.
\(
\begin{eqnarray*}
2 \int_0^{h/2} \! r\sin{\theta} \sqrt{r^2 - r^2 \sin^2{\theta}} \, r\cos{\theta}\ \mathrm{d}\theta &=& 2 \int_0^{h/2} \! r^3 \sin{\theta}\cos^2{\theta} \, \mathrm{d}\theta\\
&=& 2\left[ -\frac{1}{3} r^3 \cos^3{\theta} \right]_0^{h/2} \\
&=& -\frac{2}{3}\left[ r^3 \cos^3{\theta} \right]_0^{h/2} \\
\end{eqnarray*}
\)
Ups, batas integral masih dalam \(x\). Akan lebih mudah jika \(\theta\) dikembalikan ke \(x\). Perhatikan bahwa \(r\cos{\theta} = \sqrt{r^2 - x^2}\). Jika disubstitusi:
\(
\begin{eqnarray*}
-\frac{2}{3}\left[ r^3 \cos^3{\theta} \right]_0^{h/2} &=&-\frac{2}{3}\left[ (r^2 - x^2)^{3/2} \right]_0^{h/2}\\
\end{eqnarray*}
\)
Berhubung kalau dibuka ke bentuk tertutup rumusnya akan memusingkan, jadi saya biarkan dalam bentuk dengan batas atas dan bawah saja.
Volume akhir dari kasus kedua ini adalah 4 dikali 2 dikali, volume setengah silinder yang dikurangi bagian terpotong:
\(
\begin{eqnarray*}
V &=& 4 \left( 2\left( \left( \frac{1}{2}\pi r^2 \frac{1}{2}h \right) - \left( -\frac{2}{3}\left[ (r^2 - x^2)^{3/2} \right]_0^{h/2} \right) \right) \right)\\
&=& 8\left( \frac{1}{4} \pi r^2 h +\frac{2}{3}\left[ (r^2 - x^2)^{3/2} \right]_0^{h/2}\right)\\
\end{eqnarray*}
\)
Yap, rumus sudah didapatkan. Selanjutnya tinggal diaplikasikan ke program.




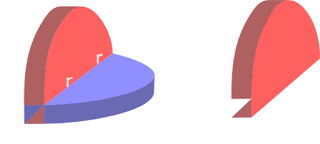

anjir goz...
BalasHapusblogspot gk ada fasilitas untuk menerjemahkan bahasa Latex ya?
BalasHapuswee... setelah di-reload lagi halamannya udah jadi jelas
Hapus